Factors of 9: Factor Pairs & Prime Factorization of 9

Factor of 9 is an important concept in mathematics, especially when dealing with multiplication and division. Understanding the factors of a number helps in simplifying problems and finding solutions.

In this article, we will define what factors are, explain how to find factors of 9 using the division method and prime factorization, and provide solved example. We will cover common factors, prime factors, and factor pairs of 9, ensuring a comprehensive understanding of this topic. Let’s dive into this article.

Part 1. What are the Factors of 9?

The factors of 9 are the numbers that can be multiplied together to yield the original number. In this section, we will explore all the factors, common factors, and prime factors of 9, answering how many factors exist.

The factors of 9 are the integers that can be multiplied together to produce 9. To find all the factors, we can check which numbers divide 9 evenly. The factors of 9 are 1, 3, and 9. Thus, the pairs of numbers that multiply to give 9 are:

• 1 × 9
• 3 × 3

#1: Common Factors of 9

Common factors are the factors that two or more numbers share. For example, the common factors of 9 and 3 are 1 and 3.

#2: Prime Factors of 9

Prime factors are the prime numbers that can be multiplied together to give the original number. A prime number is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers. The smallest prime factor of 9 is 3.

Thus, the prime factor of 9 are 3 and 3.

#3: Prime Factorization of 9

The factors of 9 can be expressed using prime factorization. The prime factorization of 9 reveals its prime factors and helps in further calculations.

The prime factorization of 9 is expressed as:

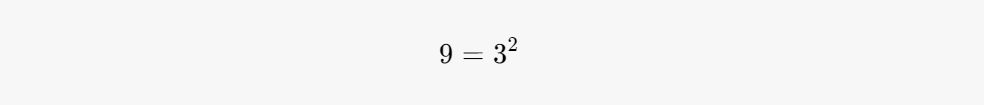
This means that 3 is multiplied by itself to yield 9.

#4: Positive Factors of 9

Positive factors are all the factors of a number that are positive integers. The positive factors of 9 are:

• 1
• 3
• 9

These factors can be paired as (1, 9) and (3, 3).

#5: Factor Pairs of 9

Factor Pairs of 9 A factor pair of 9 is a combination of two factors that can be multiplied together to get the number equals 9. For the number 9, all of the positive factors are listed below:

• 1 and 9: 1×9=9
• 3 and 3: 3×3=9

Thus, the complete list of factor pairs of 9 is:

• (1, 9)
• (3, 3)

These pair factors can be either positive or negative, as multiplying two negative numbers also yields a positive product.

#5: Negative Pair Factors of

Negative pair factors are simply the negative counterparts of the positive factor pairs. For example, the negative factor pairs of 9 are:

• (-1, -9)
• (-3, -3)

These pairs also multiply to give 9.

#5: Positive Pair Factors of 9

Positive pair factors are pairs of positive integers that multiply together to give the original number. For the number 9, the positive pair factors are:

• (1, 9): 1×9=9
• (3, 3): 3×3=9

Part 2. How to Find Factors of 9?

To find the factors of 9, we can use methods such as the factor tree and the prime factorization method. This section will guide you through the process of finding factors.

#1. How To Find Factors of 9 Using the Prime Factorization Method?

Using the prime factorization method, we can find the factors of 9 by identifying its prime factors. Since the prime factorization of 9 is 3232, the factors can be expressed as combinations of these prime factors.

Step 1: Identify the Smallest Prime Factor

Begin by identifying the smallest prime number that can divide 9 evenly. The smallest prime number larger than 1 is 2, but since 9 is odd, we move to the next prime number, which is 3.

Step 2: Divide by the Smallest Prime Factor

Now, divide 9 by 3:

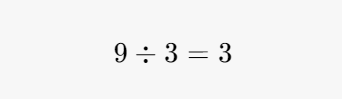
This indicates that 3 is a prime factor of 9.

Step 3: Repeat the Division

Next, take the quotient (the result of the division) and continue to divide by the smallest prime factor:

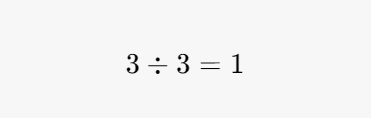
Now we have reached 1, which signals that the division process is complete.

Step 4: Write the Prime Factorization

The prime factorization of 9 can now be represented as:

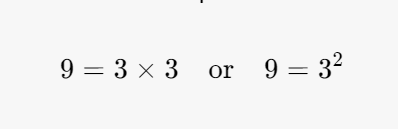
Step 5: List the Factors

From the prime factorization, you can deduce all the factors of 9. The factors are derived from the combinations of the prime factors:

Thus, the complete list of factors of 9 is: 1, 3, and 9

#2. Using Division Method to Find Factors of 9

The division method involves systematically dividing the number by its integers to identify all the factors. Here’s how to find the factors of 9 using this method. To find the prime factors of 9 using the division method, we divide 9 by the smallest prime number:

Step 1: Start with the Number

Begin with the number you want to factor, which is 9.

Step 2: Divide by Natural Numbers

Start dividing 9 by natural numbers, beginning with 1, and check for whole number results (no remainders). Here are the calculations:

Division	Calculation	Result	Factors Found
Divide by 1:	9÷1=99÷1=9	9 (no remainder)	1 and 9
Divide by 2:	9÷2=4.59÷2=4.5	4.5 (not a whole number)	No factors from this division.
Divide by 3:	9÷3=39÷3=3	3 (no remainder)	3 (already noted from previous step)
Divide by 4:	9÷4=2.259÷4=2.25	2.25 (not a whole number)	No factors from this division.
Divide by 5:	9÷5=1.89÷5=1.8	1.8 (not a whole number)	No factors from this division.
Divide by 6:	9÷6=1.59÷6=1.5	1.5 (not a whole number)	No factors from this division.
Divide by 7:	9÷7=1.28579÷7=1.2857	1.2857 (not a whole number)	No factors from this division.
Divide by 8:	9÷8=1.1259÷8=1.125	1.125 (not a whole number)	No factors from this division.
Divide by 9:	9÷9=19÷9=1	1 (no remainder)	9 (already noted from previous step)

Step 3: Compile the Factors

From the divisions where there were no remainders, we can list the factors of 9:

• 1
• 3
• 9

The factors of 9, found using the division method, are 1, 3, and 9. This method effectively identifies all the integers that can divide the number evenly, confirming the factors of 9.

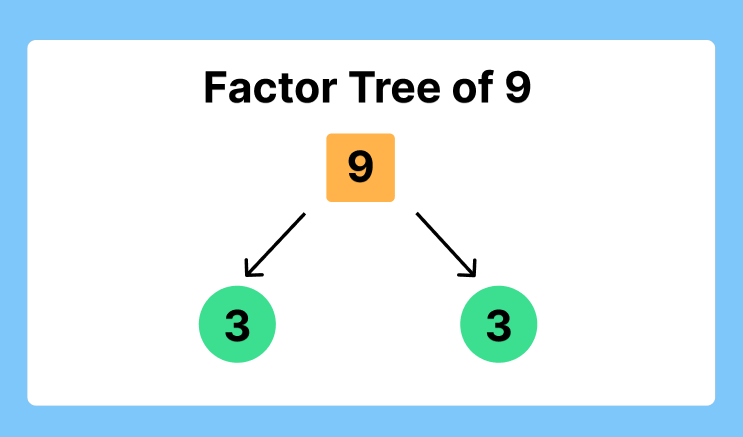
#3. Find Factors of 9 with Factor Tree Method

A factor tree is a visual representation that helps break down a number into its prime factors. Here’s how to find the factors of 9 using a factor tree:

Step 1: Start with the Number

Begin with the number 9 at the top of the factor tree.

Step 2: Divide by the Smallest Prime Factor

Identify the smallest prime factor of 9. The smallest prime factor of 9 is 3. Divide 9 by 3:

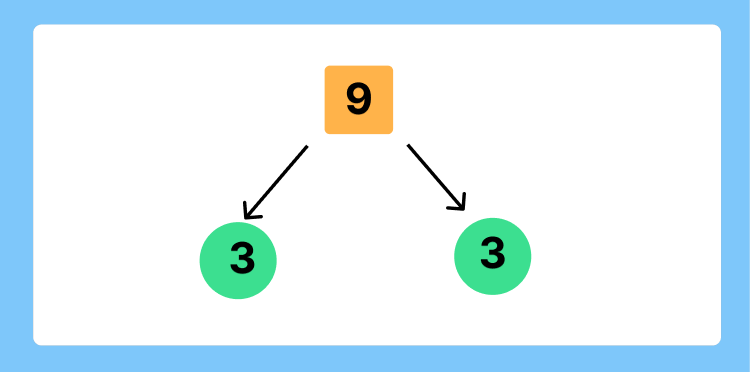
Step 3: Continue Dividing

Since both branches of the tree have reached prime numbers (3), you can stop here. The original number 9 has been broken down completely.

Step 4: Write the Prime Factorization

The prime factorization of 9 can be expressed as:

Step 5: List the Factors of 9

From the prime factorization, we can identify all the factors of 9:

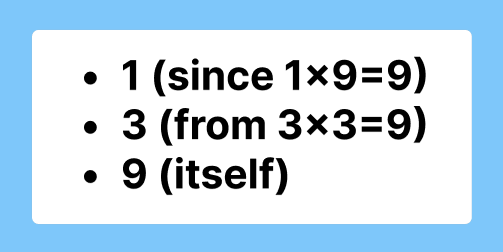
Using the factor tree method, we find that the factors of 9 are 1, 3, and 9. This method visually demonstrates how the number can be decomposed into its prime components, making it easier to understand the relationship between the factors.

Part 3. Solved Examples of Factors of 9

In this section, we present solved examples that demonstrate how to find the factors of 9.

Example 1: What are the Prime Factors of 9?

Answer:	The prime factors of 9 are 3.
Explanation:	The prime factorization of 9 involves dividing by the smallest prime number:

The prime factorization shows that

Therefore, the only prime factor is 3.

Example 2: What are the Negative Factors of 9?

Answer:	The negative factors of 9 are -1, -3, and -9.
Explanation:	Each positive factor has a corresponding negative counterpart. The negative factors are simply the negatives of the positive factors:

Frequently Asked Questions on Factors of 9

Q1: What’s the Factors of 1/9?

A: The factors of a fraction like 1/9​ can be understood in terms of its numerator and denominator.

1. Numerator (1): The factors of 1 are simply 1.
2. Denominator (9): The factors of 9 are 1, 3, and 9.

When considering the factors of 1/9​, we can think of it as the set of fractions that can be formed using these factors:

Q2: What is the lowest common factor of 6 and 9?

A: The lowest common factor is 3.

Q3: What is the lowest common factor of 4 and 9?

A: The lowest common factor is 1.

Q4: What is the lowest common factor of 9 and 12?

A: The lowest common factor is 3.

Q5: What is the greatest common factor of 9 and 15?

A: The greatest common factor is 3.

Q6: What is the sum of the first nine prime numbers?

A: The sum is 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 = 129.

Q7: Is 9 a Prime Number?

A: No, 9 is not a prime number because it has factors other than 1 and itself (specifically, it is divisible by 3).

Conclusion

Factor of 9 is a fundamental concept in mathematics that involves understanding its factors of 9, prime factors, and factor pairs. By exploring the definition, methods to find factors using techniques like the factor tree, and providing solved examples, we’ve covered the essential aspects of this topic.

Additionally, we discussed negative factors and how they relate to prime numbers. Understanding these concepts not only aids in solving mathematical problems but also enhances overall numerical literacy.