5 Hardest Math Problems on SAT with Answers

Want to test the hardest SAT math problems? Want to know what makes them so difficult and how to best solve them?

These are 5 hardest math problems from the College Board’s SAT practice tests, which means that understanding them is one of the best ways to study for those who want to prepare for the SAT or just aim for perfection.

Question 1.

The equation above shows the relationship between temperature F, measured in degrees Fahrenheit, and temperature C, measured in degrees Celsius. Based on this equation, which of the following must be true?

A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 5/9 degree Celsius.

A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.

A temperature increase of 5/9 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.

A) 1 only
B) 2 only
C) 3 only
D) 1 and 2 only

ANSWER EXPLANATION: Think of the equation as an equation for a line y = mx + b, where in this case C = 5/9(F – 32)

You can see the slope of the graph is 5/9, which means that for an increase of 1 degree Fahrenheit, the increase is 5/9 of 1 degree Celsius.

C = 5/9(F) , C = 5/9(1) = 5/9

Therefore, statement I is true. This is the equivalent to saying that an increase of 1 degree Celsius is equal to an increase of 9/5 degrees Fahrenheit.

C = 5/9(F) , 1 = 5/9(F) , (F) = 9/5

Since 9/5 = 1.8, statement 2 is true. The only answer that has both statement 1 and statement 2 as true is D, but if you have time and want to be absolutely thorough, you can also check to see if statement 3 (an increase of 5/9 degree Fahrenheit is equal to a temperature increase of 1 degree Celsius) is true: C = 5/9(F) , C = 5/9(5/9) , C = 25/81(which is ≠ 1)

An increase of 5/9 degree Fahrenheit leads to an increase of 25/81, not 1 degree, Celsius, and so Statement 3 is not true.

The final answer is D.

Question 2.

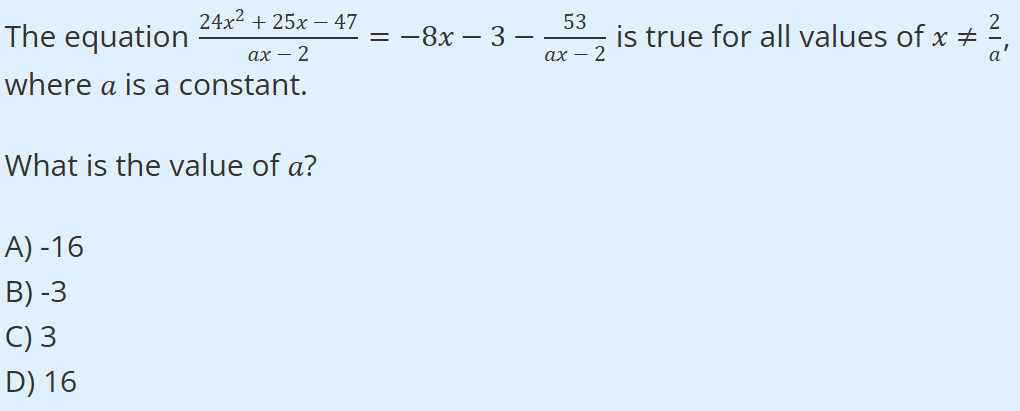
ANSWER EXPLANATION: There are two ways to solve this question. The faster way is to multiply each side of the given equation by ax − 2 (so you can get rid of the fraction). When you multiply each side by ax − 2, you should have: 24x²+ 25x – 47 = (-8x – 3) (ax – 2) – 53

You should then multiply (-8x – 3) and (ax – 2) using FOIL.

24x²+ 25x – 47 = -8ax² – 3ax + 16x + 6 – 53

Then, reduce on the right side of the equation 24x²+ 25x – 47 = -8ax² – 3ax + 16x – 47

Since the coefficients of the x² -term have to be equal on both sides of the equation, -8a = 24, or a = -3. The other option which is longer and more tedious is to attempt to plug in all of the answer choices for a and see which answer choice makes both sides of the equation equal. Again, this is the longer option, and I do not recommend it for the actual SAT as it will waste too much time.

The final answer is B.

Question 3.

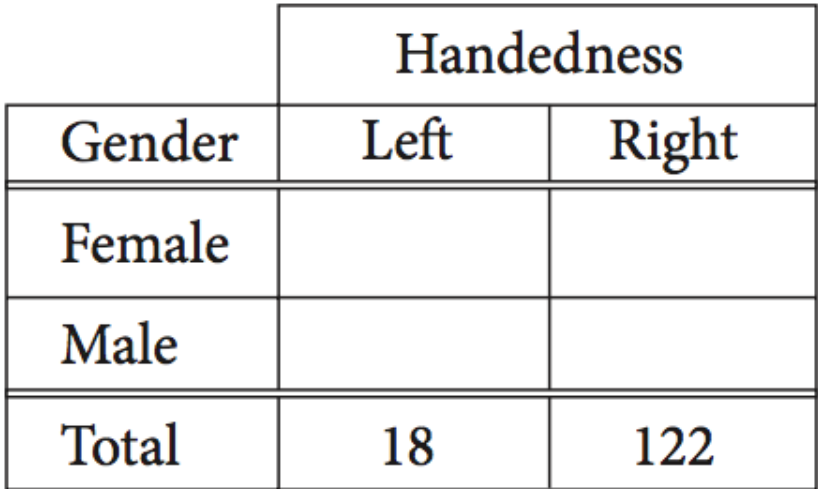
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students.

If there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)

A) 0.410

B) 0.357

C) 0.333

D) 0.250

ANSWER EXPLANATION: In order to solve this problem, you should create two equations using two variables (x and y) and the information you’re given. Let x be the number of left-handed female students and let y be the number of left-handed male students. Using the information given in the problem, the number of right-handed female students will be 5x and the number of right-handed male students will be 9y. Since the total number of left-handed students is 18 and the total number of right-handed students is 122, the system of equations below must be true:

x + y = 18

5x + 9y = 122

When you solve this system of equations, you get x = 10 and y = 8. Thus, 5*10, or 50, of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is 50/122, which to the nearest thousandth is 0.410.

The final answer is A.

Question 4.

Little’s law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spend an average of 5 minutes in the checkout line. At any time during business hours, about how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?

ANSWER EXPLANATION: Since the question states that Little’s law can be applied to any single part of the store (for example, just the checkout line), then the average number of shoppers, N, in the checkout line at any time is N = rT, where r is the number of shoppers entering the checkout line per minute and T is the average number of minutes each shopper spends in the checkout line. Since 84 shoppers per hour make a purchase, 84 shoppers per hour enter the checkout line. However, this needs to be converted to the number of shoppers per minute (in order to be used with T=5). Since there are 60 minutes in one hour, the rate is 84

shoppers per hour/60 minutes =1.4 shoppers per minute. Using the given formula with r=1.4 and T=5 yields

N=rt=(1.4)(5)=7

Therefore, the average number of shoppers, N, in the checkout line at any time during business hours is 7.

The final answer is 7.

Question 5.

The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)

ANSWER EXPLANATION: According to the original information given, the estimated average number of shoppers in the original store at any time (N) is 45. In the question, it states that, in the new store, the manager estimates that an average of 90 shoppers per hour (60 minutes) enter the store, which is equivalent to 1.5 shoppers per minute (r). The manager also estimates that each shopper stays in the store for an average of 12 minutes (T). Thus, by Little’s law, there are, on average, N=rT=(1.5)(12)=18 shoppers in the new store at any time. This is

45−18/45*100=60

percent less than the average number of shoppers in the original store at any time.

The final answer is 60.

FAQs on the Hardest Math Problems

1. What is the most difficult math section on the SAT?

The most challenging math section of the SAT is often considered the “Problem Solving and Data Analysis” section.

According to the College Board, many students typically score lower on this section than on other sections. This section requires strong skills in interpreting data, understanding ratios, and applying math concepts to real-world scenarios. Recent SAT score data shows that many students struggle with this type of question, affecting their overall score.

2. What are 7th grade math problems? [with examples]

7th grade math problems often involve concepts such as solving equations, calculating percentages, or understanding geometry. This level of math builds on prior knowledge and prepares students for more advanced topics such as algebra and geometry in high school. 7th grade math problems build on students’ reasoning skills and understanding of key mathematical concepts.

Here are some examples of 7th grade math problems:

1. Isabella got 16 out of 40 questions wrong on her quiz. What percent did she get correct?
2. Solution: 16/40 can be simplified to 2/5​, which is equivalent to 40/100​ or 40%. If Isabella got 40% incorrect, she got 60% correct (100-40=60).
3. Three out of every five students are wearing jeans. If there are 20 students in all, how many are not wearing jeans?
4. Solution: From the last problem, we saw that 3/5​ is the same as the 12 students wearing jeans. If there are 20 students total, we can subtract the 12 wearing jeans from the 20 total to find that 8 are not wearing jeans. We could also set up this proportion and solve to get 8.2/5 = x/20
5. Madison measured this angle with her protractor and said “It is 60°.” Without measuring the angle, Bella said she could tell Madison’s answer was incorrect. How did Bella know this?
6. Solution: Bella knew this angle could not be 60° because this angle is obtuse but a 60° angle is acute.

If you want to know more math knowledge, please click the links below, Wukong Education will help you improve your math ability.