30 60 90 Triangle: Calculator, Rules, Formula, Properties, Examples [2025 Ultimate Guide]
Markedly different from the common right angled triangle, the 30 60 90 triangle is the only right triangle with angles in an arithmetic progression, having three different angles: 30 degrees, 60 degrees, and 90 degrees. Geometry is based on this special triangle, which has many remarkable traits and formulas.

We will go over the 30-60-90 triangle in great detail here, including how to use a 30 60 90 triangle calculator, the main rules and formula, the characteristics of this unique right triangle, solved examples, and a free worksheet to practice 60 30 90 triangle issues.
This complete introduction to the special right triangle 30 60 90 contains all you need, regardless of your level of geometry knowledge – teacher, student, or simply inquisitive.
Discovering the maths whiz in every child,
that’s what we do.
Suitable for students worldwide, from grades 1 to 12.
Get started free!Part 1. What is 30-60-90 Right Triangle?
A 30 60 90 triangle is a particular right triangle having interior angles of 30 degrees, 60 degrees, and 90 degrees. Geometry and trigonometry find great relevance in this triangle since it possesses special qualities that distinguish it from other right-angled triangles.

Properties of 30-60-90 triangle
| 1 | The angles are 30 degrees (smallest angle), 60 degrees (mid sized degree angle), and 90 degrees. |
| 2 | The legs are in the ratio of 1:√3:2, where the shortest leg is 1, the middle leg is √3, and the longer leg is 2. |
| 3 | The hypotenuse is always twice the length of the shorter leg. |
| 4 | The middle length is always √3 times the length of the shorter leg. These properties can be derived by cutting an equilateral triangle in half, which creates two 30-60-90 triangles. |
Special Triangles 30 60 90
One of the two unique right triangles in geometry; the other is the 45 45 90 triangle (equal angles). From navigation to building, these unique triangles find application in various fields thanks to their particular qualities and formulas.
For instance, if you consider an equilateral triangle ABC, cutting it in half along the altitude creates two 30-60-90 triangles.
Designed to help you quickly answer problems with this unique right triangle, the 30 60 90 Triangle Calculator is The calculator can find the missing numbers by entering known facts, such the value of one angle or the length of one side.
Enter the length of one side:
- Short Leg (x):
- Long Leg (x√3):
- Hypotenuse (2x):
Part 2. 30 60 90 Triangle Rules
The 30 60 90 Triangle Rules are a set of rules that define the unique characteristics and linkages found within this specific right triangle. A 30-60-90 triangle follows these general guidelines:
| 1 | The angles are 30 degrees, 60 degrees, and 90 degrees (right angle). |
|---|---|
| 2 | The leg length is in the ratio of 1:√3:2, where the shortest leg is 1, the medium leg is √3, and the long leg is 2. |
| 3 | The hypotenuse is always twice the length of the shortest leg. |
| 4 | The medium length is always √3 times the length of the short leg. |
| 5 | If the shortest leg is known, the other two legs can be easily calculated using the ratios. |
Consider triangle ABC, where the angles are 30 degrees, 60 degrees, and 90 degrees; the rules of the 30 60 90 triangle apply directly to this triangle.
For example, if the shortest leg of a 30 60 90 triangle is 6 units, then:
- The medium leg would be 6√3 ≈ 10.39 units.
- The largest side would be 12 units.
From engineering and construction to navigation and trigonometry, these guidelines make the 90 60 30 triangle a practical instrument in many fields.
Part 3. 30 60 90 Triangle Formula
The 30 60 90 Triangle Formula describes the mathematical relationships between the legs and angles of this special right triangle. These formulas and recommendations for the 30, 60, and 90 triangle provide a comprehensive set of tools for dealing with scenarios involving this special triangle.
| Formula | Description |
|---|---|
| a = x b = x√3 c = 2x | Where ‘a’ is the short side, ‘b’ is the medium side, ‘c’ is the longest side, and ‘x’ is the length of the shortest side. |
| sin 30° = 1/2 cos 30° = √3/2 tan 30° = 1/√3 | The trigonometric ratios for the 30-degree angle. |
| sin 60° = √3/2 cos 60° = 1/2 tan 60° = √3 | The trigonometric ratios for the 60-degree angle. |
| sin 90° = 1 cos 90° = 0 tan 90° = undefined | The trigonometric ratios for the 90-degree angle. |
Part 4. 30 60 90 Triangle Three Sides
A 30 60 90 triangle’s side lengths follow a precise ratio that makes this triangle a handy instrument in many different fields.
By drawing a perpendicular from one vertex of an equilateral triangle to the opposite side, you create triangle ABD, which is a 30-60-90 triangle.
A 30 60 90 triangle’s side lengths fall in the ratio 1:√3:2, whereby:
- The shortest side has a length of 1 unit.
- The medium side has a length of √3 units.
- The longest side (the hypotenuse) has a length of 2 units.
What are the ratios of a 30 60 90 Triangle?

The triangle’s angles of 30 degrees, 60 degrees, and 90 degrees produce this ratio directly. Therefore, once you identify the medium-length angle, you can quickly pinpoint the remaining angle equal to 30 degrees.
Thirty sixty ninety triangle ratios.
A 30 60 90 triangle has sides with ratios as follows:
- Shortest side (a) : Medium side (b) : Longest side (c) = 1 : √3 : 2
- a = 1 unit
- b = √3 units
- c = 2 units
As long as the angles stay 30 degrees, 60 degrees, and 90 degrees, these ratios are consistent relationship of the triangle’s real size.
Part 5. 30-60-90 Triangle Calculator
The 30-60-90 triangle calculator is a powerful tool designed to simplify solving problems involving this special right triangle. This tool is especially useful for quickly solving problems involving right triangles, making it an essential resource for anyone working with 30 60 90 triangles. Whether you’re a student, teacher, or professional, this calculator can help you quickly find the lengths of the sides, the area, and other properties of the triangle.
For example, if you want to find the lengths of the sides of a 30-60-90 triangle with a hypotenuse of 10 inches, you would enter “10” in the “Hypotenuse” field, choose “inches” as the unit of measurement, and click the “Calculate” button. The calculator would then display the lengths of the other sides: the shortest side would be 5 inches, and the middle length side would be 5√3 inches.
30-60-90 Triangle Calculator
Enter the length of one side:
Results:
Part 3. 30 60 90 Triangle Formula
The 30 60 90 Triangle Formula describes the mathematical relationships between the legs and angles of this special right triangle. These formulas and recommendations for the 30, 60, and 90 triangle provide a comprehensive set of tools for dealing with scenarios involving this special triangle.
| Formula | Description |
|---|---|
| a = x b = x√3 c = 2x | Where ‘a’ is the short side, ‘b’ is the medium side, ‘c’ is the longest side, and ‘x’ is the length of the shortest side. |
| sin 30° = 1/2 cos 30° = √3/2 tan 30° = 1/√3 | The trigonometric ratios for the 30-degree angle. |
| sin 60° = √3/2 cos 60° = 1/2 tan 60° = √3 | The trigonometric ratios for the 60-degree angle. |
| sin 90° = 1 cos 90° = 0 tan 90° = undefined | The trigonometric ratios for the 90-degree angle. |
Part 5. Solved Examples and Practice Problems (With Worksheet)
Solved Examples
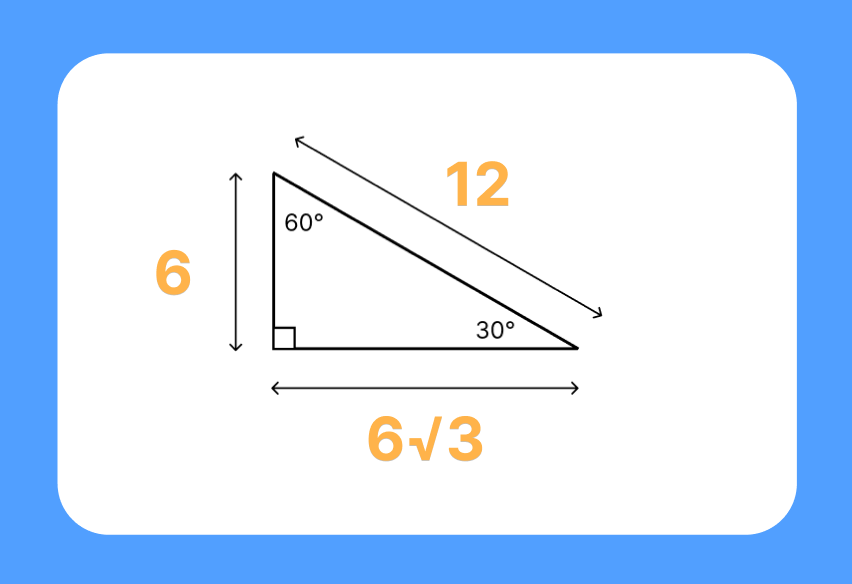
Question 1. Find the missing side lengths of a 30 60 90 triangle if the shortest side is 6 units.
- Given: Shortest side (a) = 6 units
- Using the 30 60 90 triangle formulas:
- Medium side (b) = a√3 = 6√3 ≈ 10.39 units
- Longest side (c) = 2a = 2 × 6 = 12 units
Question 2. In a 30 60 90 triangle, the hypotenuse is 10 units. Find the lengths of the other two sides.
- Given: Hypotenuse (c) = 10 units
- Using the 30 60 90 triangle formulas:
- Shortest side (a) = c/2 = 10/2 = 5 units
- Medium side (b) = a√3 = 5√3 ≈ 8.66 units

Question 3. The medium side of a 30 60 90 triangle is 12 units. Find the lengths of the other two sides.
- Given: Medium side (b) = 12 units
- Using the 30 60 90 triangle formulas:
- Shortest side (a) = b/√3 = 12/√3 ≈ 6.93 units
- Longest side (c) = 2b = 2 × 12 = 24 units

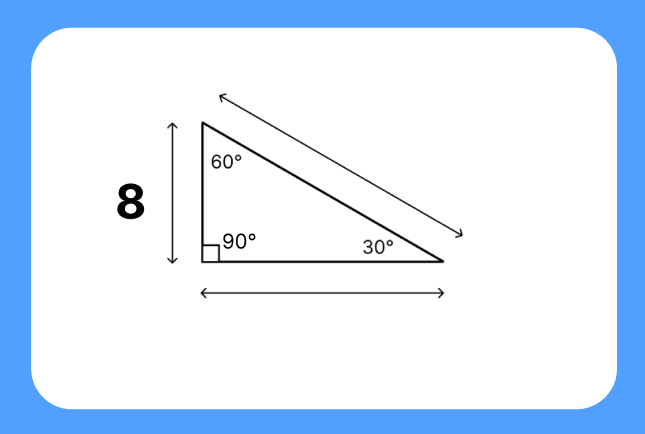
Question 4. The shortest side of a 30 60 90 triangle is 8 units. Find the angle measures.
- Given: Shortest side (a) = 8 units
- Using the 30 60 90 triangle rules:
- Angle 1 = 30 degrees
- Angle 2 = 60 degrees
- Angle 3 = 90 degrees
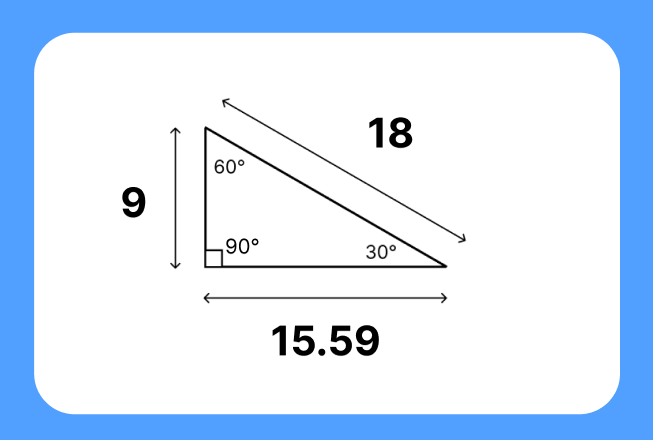
Question 5. The longest side of a 30 60 90 triangle is 18 units. Find the lengths of the other two sides.
- Given: Longest side (c) = 18 units
- Using the 30 60 90 triangle formulas:
- Shortest side (a) = c/2 = 18/2 = 9 units
- Medium side (b) = a√3 = 9√3 ≈ 15.59 units
Practice Problems
30 60 90 Triangle Worksheet – Download for free
To further practice working with 30 60 90 triangles, you can download a free worksheet here: [link to worksheet].
FAQ
Q1. What is 30-60-90 triangle unit circle?
In trigonometry, the 30 60 90 triangle has tight relationship with the unit circle. Coordinates of the points corresponding to the 30-degree, 60-degree, and 90-degree angles on the unit circle are:
- 30 degrees: (√3/2, 1/2)
- 60 degrees: (1/2, √3/2)
- 90 degrees: (0, 1)
The x-coordinate denotes the adjacent side, the y-coordinate the opposite side, and the hypotenuse is always 1 (the radius of the unit circle), so these coordinates are exactly connected to the side lengths of the 30 60 90 triangle.
Q2. How do I find the trigonometric ratios in a 30-60-90 triangle?
| Angle | Sine | Cosine | Tangent |
|---|---|---|---|
| 30° | 1/2 | √3/2 | 1/√3 |
| 60° | √3/2 | 1/2 | √3 |
Q3. What are some practical applications of 30-60-90 triangles?
- Roof construction (the 30-60-90 triangle is often used in the design of roofs)
- Electrical engineering (the 30-60-90 triangle is used in the analysis of three-phase electrical systems)
- Navigation (the 30-60-90 triangle is used in determining direction and distance)
Q4. How can I use the properties of 30-60-90 triangles to solve problems?
- Identify if a triangle is a 30-60-90 triangle.
- Use the side length relationships to find unknown side lengths.
- Apply the trigonometric ratios to solve for angles or other values.
- Utilize the properties in real-world applications, such as in construction or engineering.
Conclusion
In geometry and trigonometry, the 30 60 90 triangle is ultimately a particular right triangle with peculiar qualities and formulas that make it significant. Including definition, properties, calculator, rules, formulas, side lengths, and solved examples, this thorough tutorial has addressed the main features of the 30-60-90 triangle.

Understanding the subtleties of this unique triangle can help you to answer many kinds of mathematical problems and apply this knowledge in many spheres, including navigation and beyond as well as building and engineering. The 30 60 90 triangle is a great addition to your mathematical toolkit regardless of your level of geometry knowledge – that of a teacher, student, or merely an interested person.
If you’d like to study more about triangles or geometry, WuKong Math offers an online small-class math course. New users can attend a 1-on-1 online course taught by a well-known teacher, and once completed, they will have access to a variety of online learning resources about geometry.
Discovering the maths whiz in every child,
that’s what we do.
Suitable for students worldwide, from grades 1 to 12.
Get started free!Delvair holds a degree in Physics from the Federal University of Maranhão, Brazil. With over six years of experience, she specializes in teaching mathematics, with a particular emphasis on Math Kangaroo competitions. She firmly believes that education is the cornerstone of society’s future. Additionally, she holds the conviction that every child can learn given the right environment and guidance. In her spare time, she enjoys singing and tending to her plants.




![How to Learn Abacus Maths at Home [2025 Guide] How to Learn Abacus Maths at Home [2025 Guide]](https://wp-more.wukongedu.net/blog/wp-content/uploads/2024/01/image-142-520x293.jpeg)



![5th Grade Math Test: Strategies & Free Practice Tests [2025 Updated] 5th Grade Math Test: Strategies & Free Practice Tests [2025 Updated]](https://wp-more.wukongedu.net/blog/wp-content/uploads/2024/02/image-19-520x293.jpeg)











![Greater Than Sign, Less Than, Equal Symbols [Examples & Meaning] Greater Than Sign, Less Than, Equal Symbols [Examples & Meaning]](https://wp-more.wukongedu.net/blog/wp-content/uploads/2025/01/image-633-520x293.png)
![How Many Weeks in a Year? Calculation and Table [2025 Step-by-Step Guide] How Many Weeks in a Year? Calculation and Table [2025 Step-by-Step Guide]](https://wp-more.wukongedu.net/blog/wp-content/uploads/2024/08/image-144-520x293.png)




Comments0
Comments