How to Find GCF(Greatest Common Factor)?

The Greatest Common Factor (GCF), also known as the greatest common divisor (GCD) or highest common factor (HCF), is the largest positive integer that divides two or more non-zero integers without leaving a remainder.

Finding the GCF is a fundamental skill in mathematics, particularly useful in simplifying fractions, solving equations, and various other applications.

In this article, we will explore different methods to find the GCF, including listing factors, prime factorization, and the division method, and provide examples and practice questions to help you master this concept.

What is Greatest Common Factor (GCF)?

The GCF of two or more integers is the largest number that can divide each of them exactly. For example, the GCF of 12 and 18 is 6, as 6 is the highest number that divides both 12 and 18 without a remainder.

How to Find GCF?

There are several methods to find the GCF of numbers. Let’s explore the most common ones.

GCF by Listing Factors

This method involves listing all the factors of each number and then identifying the largest common factor.

Steps:

1. Find all the factors of each number.
2. Identify the common factors.
3. The largest of these common factors is the GCF.

Example:

Find the GCF of 24 and 36.

• Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
• Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
• Common factors: 1, 2, 3, 4, 6, 12
• GCF: 12

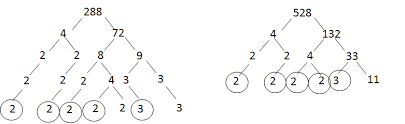
GCF by Prime Factorization

Prime factorization involves breaking down each number into its prime factors. The GCF is found by multiplying the lowest power of each common prime factor.

Steps:

1. Find the prime factorization of each number.
2. Identify the common prime factors.
3. Multiply the lowest power of each common prime factor to get the GCF.

Example:

Find the GCF of 48 and 72.

• Prime factors of 48: 24×3
• Prime factors of 72: 23×32
• Common prime factors: 2 and 3
• Lowest powers: 23 and 3
• GCF: 23×3=8×3=24

Finding GCF by Division Method (Euclidean Algorithm)

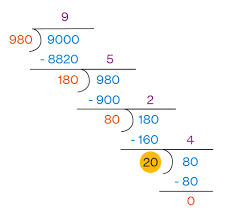
The division method, or Euclidean algorithm, involves dividing the larger number by the smaller number and repeating the process with the remainder until the remainder is zero. The last non-zero remainder is the GCF.

Steps:

1. Divide the larger number by the smaller number.
2. Divide the divisor by the remainder obtained in the previous step.
3. Repeat until the remainder is zero.
4. The last non-zero remainder is the GCF.

Example:

Find the GCF of 108 and 72.

• Divide 108 by 72: Quotient = 1, Remainder = 36
• Divide 72 by 36: Quotient = 2, Remainder = 0
• GCF: 36

GCF and LCM

The GCF and LCM (Least Common Multiple) are related concepts but serve different purposes.

Difference between GCF and LCM

• GCF: The largest number that divides two or more numbers without a remainder.
• LCM: The smallest number that is a multiple of each of the numbers.

Example:

For numbers 8 and 12:

• GCF: 4
• LCM: 24

Greatest Common Factor Examples

Let’s look at more examples to solidify our understanding.

Example	Numbers	Method	GCF
1	36 and 48	Prime Factorization	12
2	60, 90, 150	Division Method	30
3	56 and 98	Listing Factors	14

Example 1: GCF of 36 and 48 using Prime Factorization

• Prime factors of 36: 22×32
• Prime factors of 48: 24×3
• Common prime factors: 2 and 3
• Lowest powers: 22 and 3
• GCF: 22×3=4×3=12

Example 2: GCF of 60, 90, and 150 using Division Method

1. GCF of 60 and 90:
   • Divide 90 by 60: Quotient = 1, Remainder = 30
   • Divide 60 by 30: Quotient = 2, Remainder = 0
   • GCF: 30
2. GCF of 30 and 150:
   • Divide 150 by 30: Quotient = 5, Remainder = 0
   • GCF: 30

Example 3: GCF of 56 and 98 using Listing Factors

• Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
• Factors of 98: 1, 2, 7, 14, 49, 98
• Common factors: 1, 2, 7, 14
• GCF: 14

Practice Questions on GCF

1. Find the GCF of 27 and 45 using the prime factorization method.
2. Determine the GCF of 72 and 90 by listing factors.
3. Use the division method to find the GCF of 144 and 192.
4. What is the GCF of 15, 25, and 35? Show your work using any method of your choice.
5. Find the GCF of 100 and 125 and explain the steps you took.

FAQ About Greatest Common Factor

What is the easiest way to find the GCF?

The easiest way to find the GCF is by listing factors. First, list all factors of each number. Then, identify the common factors. Finally, select the largest common factor from the list. This method is simple and effective for small numbers.

How to find the greatest common of 24 and 36?

The GCD of 24 and 36 can be found through prime factorization. Decompose each number into primes: 24 = 2³×3, 36 = 2²×3². Multiply the lowest powers of common primes: 2²×3 = 12. So, GCD (24, 36) = 12.

What is the lcm of 75, 90, and 125 by prime factorization method?

2250

Are the prime numbers 1 to 100?

There are 25 prime numbers between 1 to 100 which are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Conclusion

Mastering the concept of GCF is essential in mathematics. By understanding and practicing the different methods to find the GCF, you can efficiently solve various mathematical problems.

Whether you’re working with fractions, algebraic equations, or real-world applications, knowing how to find the GCF will greatly enhance your mathematical skills and understanding.

If you still want to learn more math, you can click on the link below and WuKong Education will continue to accompany you in your studies.