Adding and Subtracting Fractions

In the world of mathematics, fractions play a crucial role. Whether you’re a student trying to solve a math problem or someone dealing with everyday situations like cooking or budgeting, understanding how to add and subtract fractions is an essential skill.

This article will guide you through the process of adding and subtracting fractions, provide helpful examples, and highlight the importance of mastering these fraction operations.

How to Add and Subtract Fractions

Adding and subtracting fractions is a fundamental math skill that involves working with both the numerator (top numbers) and denominators (bottom numbers). Let’s explore the methods in detail.

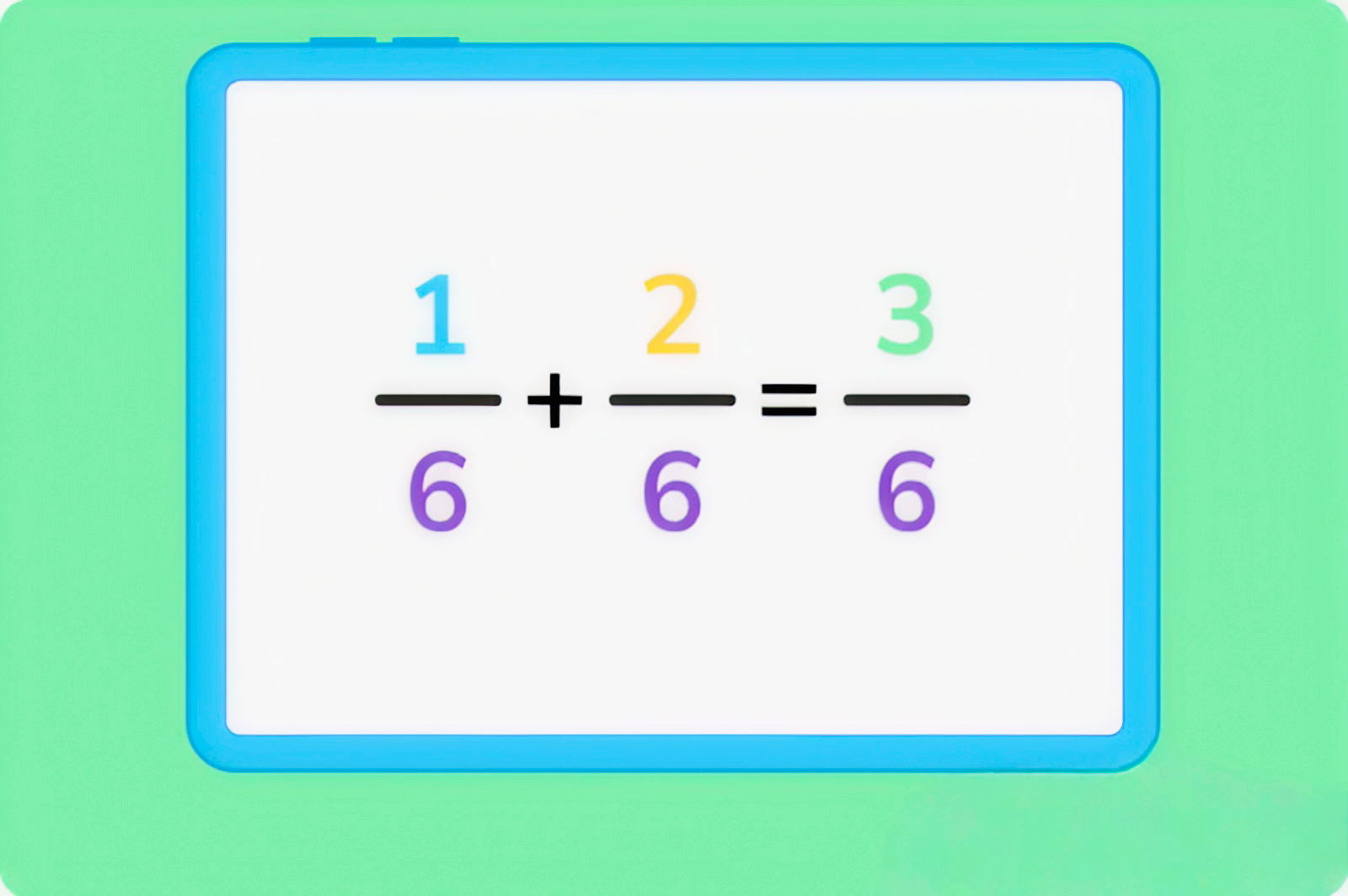
With Like Denominators

When you have fractions with the same denominator, often referred to as like denominators, the process is straightforward. You simply add or subtract the numerators while keeping the denominator unchanged.

For example, if you have 1/4 + 2/4, you add the numerators (1 + 2) to get 3, and the denominator remains 4, resulting in 3/4.

The same principle applies to subtraction.

If you subtract 1/4 from 3/4, you get 2/4, which can be simplified to 1/2.

This method works because the fractions are already divided into equal parts, making the calculation intuitive.

Here’s a table to illustrate adding and subtracting fractions with like denominators:

Fraction A	Fraction B	Addition	Subtraction
1/5	2/5	3/5	1/5
3/8	1/8	4/8 = 1/2	2/8 = 1/4
2/7	4/7	6/7	2/7

With Unlike Denominators

The process becomes slightly more complex when dealing with unlike denominators. In such cases, you need to find a common denominator before performing the addition or subtraction. For example, consider adding 1/3 and 1/6.

To do this, you need to find the least common denominator (LCD), which is the smallest multiple that both denominators can divide into.

In this case, the LCD is 6.

You then convert each fraction to an equivalent fraction with the denominator of 6.

So, 1/3 becomes 2/6, and 1/6 remains the same.

Now you can add them as before: 2/6 + 1/6 = 3/6, which simplifies to 1/2.

The key here is understanding that equivalent fractions have the same value but different numerators and denominators.

Another example: subtract fractions 3/4 and 1/6.

First, find the LCD of 4 and 6, which is 12.

Convert the fractions:

3/4 = 9/12 (multiply both numerator and denominator by 3)

1/6 = 2/12 (multiply both numerator and denominator by 2)

Now subtract: 9/12 – 2/12 = 7/12

Here’s a table to illustrate adding and subtracting fractions with unlike denominators:

Fraction A	Fraction B	LCD	Equivalent Fraction A	Equivalent Fraction B	Addition	Subtraction
1/3	1/6	6	2/6	1/6	3/6 = 1/2	1/6
2/5	1/4	20	8/20	5/20	13/20	3/20
3/8	1/6	24	9/24	4/24	13/24	5/24

Creating Common Denominators

To add or subtract fractions with different denominators, you need to create common denominators. This involves finding a common multiple of the denominators and converting each fraction to an equivalent fraction with that common denominator.

The least common denominator (LCD) is the smallest such multiple, making the calculations more efficient.

For example, let’s add 2/3 and 5/4.

The denominators are 3 and 4. The LCD of 3 and 4 is 12.

Convert each fraction:

2/3 = 8/12 (multiply numerator and denominator by 4)

5/4 = 15/12 (multiply numerator and denominator by 3)

Now add: 8/12 + 15/12 = 23/12

This can be written as a mixed number: 1 11/12.

Working With Improper Fractions and Mixed Numbers

Improper fractions are fractions where the numerator is greater than or equal to the denominator, such as 5/4 or 7/3. Mixed numbers are a combination of a whole number and a proper fraction, like 1 1/2 or 2 3/4.

To add or subtract mixed numbers, you can either convert them to improper fractions first or perform the operations separately on the whole numbers and the fractions.

For example, let’s add 1 1/2 and 2 3/4.

Method 1: Convert to improper fractions.

1 1/2 = 3/2

2 3/4 = 11/4

Find LCD of 2 and 4, which is 4.

Convert 3/2 to 6/4.

Add: 6/4 + 11/4 = 17/4 = 4 1/4.

Method 2: Add whole numbers and fractions separately.

Add whole numbers: 1 + 2 = 3.

Add fractions: 1/2 + 3/4.

Find LCD of 2 and 4, which is 4.

Convert 1/2 to 2/4.

Add: 2/4 + 3/4 = 5/4 = 1 1/4.

Combine whole number and fraction: 3 + 1 1/4 = 4 1/4.

Both methods yield the same result.

How to Work With Negative Fractions

Negative fractions add another layer of complexity to fraction operations. Understanding how to work with them is essential for solving a wide range of mathematical problems.

Rules for Math With Negative Numbers

When adding and subtracting negative fractions, the same rules apply as with negative whole numbers. If you’re adding two negative fractions, the result is a more negative fraction. For example, (-1/4) + (-1/4) = -2/4, which simplifies to -1/2.

When subtracting a negative fraction, it’s equivalent to adding the positive counterpart. For instance, 1/4 – (-1/4) is the same as 1/4 + 1/4 = 2/4 = 1/2.

Keeping these rules in mind helps prevent common errors when dealing with negative fractions.

Why Is It Important to Understand Fractions?

Understanding fractions is not just about passing a math test; it’s a skill that has practical applications in everyday life. From cooking and baking, where precise measurements are crucial, to budgeting and financial planning, fractions help us make sense of parts of a whole.

In academic settings, a solid grasp of fractions is foundational for more advanced topics like algebra, geometry, and calculus. Students who excel in fraction operations tend to have an easier time transitioning to higher-level mathematics.

Practice Makes Perfect

To truly master adding and subtracting fractions, practice is essential. Fraction worksheets offer a variety of problems that allow you to apply the concepts you’ve learned.

These worksheets often include exercises with both like and unlike denominators, as well as problems involving negative fractions.

By working through these problems, you can reinforce your understanding and identify areas where you may need additional support.

Additionally, practicing fraction operations helps improve your overall math skill and confidence.

Here’s an example of a fraction worksheet problem:

Problem: Add the fractions 3/8 and 1/6.

Solution:

Find the LCD of 8 and 6, which is 24.

Convert each fraction:

3/8 = 9/24 (multiply numerator and denominator by 3)

1/6 = 4/24 (multiply numerator and denominator by 4)

Add: 9/24 + 4/24 = 13/24.

Answer: 13/24.

Another example:

Problem: Subtract the fractions 5/7 and 2/3.

Solution:

Find the LCD of 7 and 3, which is 21.

Convert each fraction:

5/7 = 15/21 (multiply numerator and denominator by 3)

2/3 = 14/21 (multiply numerator and denominator by 7)

Subtract: 15/21 – 14/21 = 1/21.

Answer: 1/21.

Strategies for Success

When working with fractions, several strategies can help you achieve accurate results:

1. Simplify First: If possible, simplify the fractions before performing operations. This can make the calculations easier.
2. Use Visual Aids: Drawing fraction circles or bars can help visualize the fractions and understand the operations better.
3. Check Your Work: After performing the operations, use an adding and subtracting fractions calculator to verify your results.
4. Practice Regularly: The more you practice, the more comfortable you’ll become with fraction operations.

Understanding Fraction Equivalence

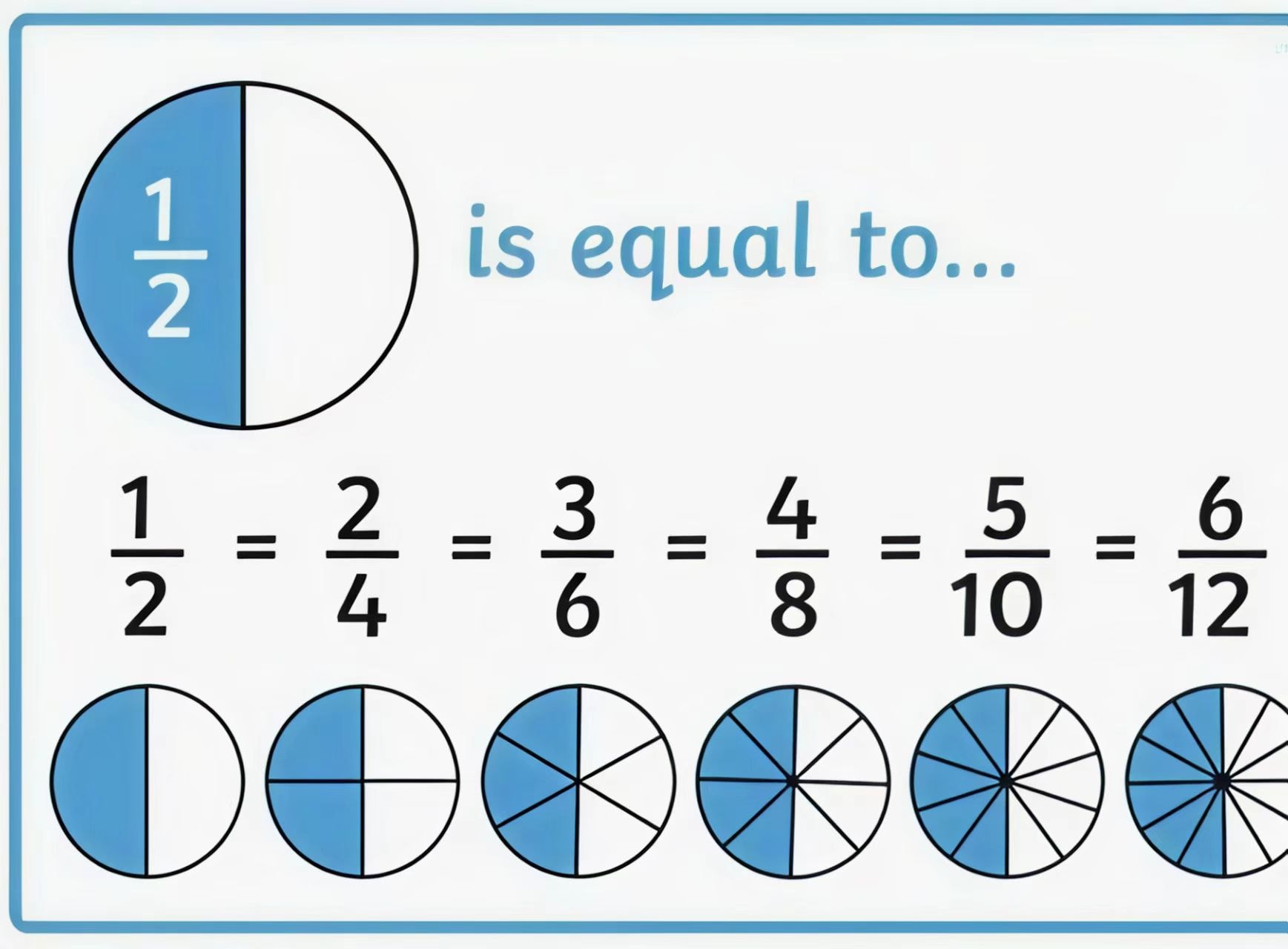
Equivalent fractions are fractions that have the same value but different numerators and denominators.

For example, 1/2 and 2/4 are equivalent fractions. Understanding equivalent fractions is crucial because it allows you to convert fractions to common denominators for addition and subtraction.

To find equivalent fractions, you can multiply or divide both the numerator and denominator by the same number. For instance:

1/2 = 2/4 = 3/6 = 4/8, and so on.

This concept is particularly useful when creating common denominators for unlike fractions.

Converting Between Improper Fractions and Mixed Numbers

Being able to convert between improper fractions and mixed numbers is another important skill. To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the numerator of the fractional part, and the denominator remains the same.

For example, let’s convert 11/4 to a mixed number:

Divide 11 by 4. The quotient is 2 and the remainder is 3.

So, 11/4 = 2 3/4.

To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and place the result over the original denominator.

For example, let’s convert 2 3/4 to an improper fraction:

Multiply 2 by 4 (2 × 4 = 8), add 3 (8 + 3 = 11), and place over 4.

So, 2 3/4 = 11/4.

The Importance of Simplifying Fractions

After adding or subtracting fractions, it’s often necessary to simplify the result to its lowest terms. Simplifying a fraction involves dividing both the numerator and denominator by their greatest common divisor (GCD). This ensures the fraction is in its simplest form.

For example, let’s simplify 8/12:

The GCD of 8 and 12 is 4.

Divide both numerator and denominator by 4: 8 ÷ 4 = 2, 12 ÷ 4 = 3.

So, 8/12 simplifies to 2/3.

Simplifying fractions makes them easier to work with and understand.

Real-World Applications

Understanding how to add and subtract fractions is not just limited to the classroom. These skills have numerous real-world applications:

1. Cooking and Baking: Recipes often require precise measurements involving fractions. If you need to double or halve a recipe, you’ll need to add or subtract fractions.
2. Budgeting: When managing finances, you might need to calculate fractions of your income or expenses.
3. Construction and DIY Projects: Measurements in construction often involve fractions, especially when working with inches or other fractional units.
4. Science and Engineering: Many scientific and engineering calculations involve fractions, particularly when working with ratios and proportions.

Fraction Operations in Higher Mathematics

A strong foundation in fraction operations is essential for success in higher mathematics. Concepts learned in basic fraction arithmetic form the building blocks for more advanced topics:

1. Algebra: Working with algebraic fractions involves similar principles to adding and subtracting numerical fractions.
2. Geometry: Fractions are used to calculate areas, volumes, and other geometric measurements.
3. Calculus: Fraction operations are necessary when working with limits, derivatives, and integrals.
4. Statistics: Fractions are used to represent probabilities and statistical data.

Supporting Students’ Learning

For teachers and parents, supporting students in learning fraction operations is crucial. Here are some ways to provide effective support:

1. Use Visual Aids: Tools like fraction circles, bars, and number lines can help students visualize fractions and understand operations better.
2. Incorporate Real-World Examples: Relating fraction problems to real-life situations makes the concepts more tangible and engaging.
3. Provide Practice Opportunities: Regular practice with fraction worksheets and exercises helps reinforce learning.
4. Encourage Questions: Create an environment where students feel comfortable asking questions and seeking clarification.
5. Utilize Technology: Fraction calculators and educational apps can supplement traditional teaching methods and provide interactive learning experiences.

FAQ About Adding and Subtracting Fractions

How do you add fractions step by step?

To add fractions, first check if denominators are the same. If not, find a common denominator. Adjust numerators accordingly. Add numerators while keeping the common denominator. Simplify the result if possible.

How do I add two fractions with different denominators?

To add two fractions with different denominators, find the least common denominator (LCD), convert each fraction to an equivalent one with the LCD, then add the numerators while keeping the denominator the same. Simplify if needed.

Conclusion

Adding and subtracting fractions may seem challenging at first, but with a clear understanding of the principles and plenty of practice, it becomes second nature.

Whether you’re working with like denominators, unlike denominators, or negative fractions, the strategies outlined in this article provide a solid foundation. Remember that tools like adding and subtracting fractions calculators can be helpful, but they should complement, not replace, your understanding.

So, embrace the practice, and soon you’ll be solving fraction problems with ease, ready to tackle more complex mathematical challenges. By mastering fraction operations, you’ll not only excel in math but also gain valuable skills applicable to various aspects of life.

If you want to learn more math knowledge, click the link below, and Wukong Education will always be with you in your learning journey.